Merkle Trees store a hash of the sub-tree in each of the Nodes, so that the whole tree’s contents can be validated against tampering.
They are used, for example, in Bitcoin’s blockchain, and in Cassandra to validate replicas.
In this article, we will show how to implement a generic Merkle Tree using features of Modern C++.

Previous implementation

A few years ago, we had shown a simplified implementation of Merkle Trees: that one worked, but had a few shortcomings; most notably, using “raw” const char* pointers, it shifted a lot of burden on the client code to keep track of where the data was, when and how to allocate it and, most importantly, how to deallocate it once done.

It also restricted the user’s options in defining a hashing function (by requiring it to return a const char *) and specifying the length of the hash result at compile time:

template <typename T, char* (hash_func)(const T&), 
    size_t hash_len>
class MerkleNode;

This code has now been completely revised and updated to take full advantage of C++11’s smart pointers, and making the hashing function fully customizable by the user: the code [is available as part of my “Distributed System Library”]()

Merkle Trees

The concept of a Merkle Tree is pretty simple: each leaf node contains the data, and a hash of the data: the hashing function can be anything the application requires, from a simple accumulation of the bytes values into a long, to a strong, secure cryptographic signature, computed using secret keys (such as SHA-256).

Non-leaf nodes contain links to their children nodes, as well as the hash of a “concatenation” of the children’s hashes (“concatenation” here defined rather loosely, as an arbitrary way to combine two hash values).

By using this structure, it is possible to validate a single data point (in the blockchain, a single Transaction) very efficiently, using only 2 log₂(N) operations, if there are N leaves; additionally, only the root hash needs to be exchanged, as every computation node can recalculate the entire tree (given the N data values, and the shared hashing function) and validate whether any of the data values have been tampered with (or added or removed).

As mentioned, Merkle trees are used in the Blockchain and are described in greater detail in Mastering bitcoin (Chapter 7, “Merkle Trees”).

Modern C++ implementation of Merkle Trees

By modifying the definition of the MerkleNode as follows:

template<typename T, typename U,
     U (Hash)(const T &),
     U (HashNode)(const shared_ptr<U> &,
                  const shared_ptr<U> &)
>
class MerkleNode;

Listing 1 — MerkleNode.hpp

we allow users of the library to define arbitrarily not only the type of the data stored in the node (T), but also the type returned by the hashing function Hash (U), as well as the “concatenate & hash” function for parent nodes (HashNode).

Additionally, as the implementation now uses exclusively shared_ptrs and does not use “raw new” anywhere (following C++11 best practice), the client code does not need to worry about allocation and deallocation of memory, nor about data getting out of scope, or being deleted twice.

You can see example usage here:

// Define a simple concatenation of the two buffers.
string ConcatHashes(const shared_ptr<string> &psl,
                    const shared_ptr<string> &psr) noexcept {
  if (!(psl || psr)) return "";
  return !psl ? *psr : !psr ? *psl : *psl + *psr;
}

/**
 * An implementation of a Merkle Tree with the nodes' elements ``strings`` and their hashes
 * computed using the MD5 algorithm.
 *
 * This is an example of how one can build a Merkle tree given a concrete type and an arbitrary
 * hashing function.
 *
 * utils::hash_str computes the MD5 of a string, and returns the result as a std::string.
 */
using MD5StringMerkleNode = MerkleNode<std::string, std::string, utils::hash_str, ConcatHashes>;

int main() {

  // Build the nodes' data.
  vector<string> nodes;
  nodes.reserve(num_nodes);
  for (int i = 0; i < num_nodes; ++i) {
    nodes.push_back("node #" + std::to_string(i));
  }

  // Build the tree from the data.
  auto root = merkle::Build<string, string, utils::hash_str, ConcatHashes>(values);

  // Ensure the tree has been built correctly.
  return root->IsValid() ? EXIT_SUCCESS : EXIT_FAILURE;

Listing 2 — merkle_demo.cpp

A couple of things worth noting:

• the actual tree is held simply via a reference to its root, the use of shared_ptrs ensures that the data will not be deallocated, as long as it’s used and root is in-scope;
• all the work in building the tree is done in merkle::Build(), which we’ll see in a second, and the data is stored in the tree’s leaves: if we were using this in a similar fashion as Bitcoin’s blockchain, we would only have to transmit the root’s computed Hash (alongside, obviously, the data contained in the nodes vector): the receiver could use merkle::Build(nodes) similarly, and then compare its own computed root hash with the received one and thus validate the received data against tampering.

Building a Merkle Tree

The code to build a tree from a vector of T data is pretty straightforward:

template<typename T, typename U,
     U (Hash)(const T &),
     U (HashNode)(const shared_ptr<U> &, const shared_ptr<U> &)
>
std::unique_ptr<MerkleNode<T, U, Hash, HashNode>> Build(const std::vector<T> &values) {

  if (values.empty()) {
    throw merkle_tree_invalid_state_exception{"Cannot build a MerkleTree with an empty vector"};
  }

  auto root = std::make_unique<MerkleNode<T, U, Hash, HashNode>>(values[0]);
  auto pos = values.begin() + 1;
  while (pos != values.end()) {
    root = std::move(AddLeaf<T, U, Hash, HashNode>(std::move(root), *pos));
    pos++;
  }
  return root;
}

Listing 3 — merkle::Build()

it takes advantage of the MerkleNode::AddLeaf() method, which computes the necessary hashes and fills in the tree:

template<typename T, typename U,
     U (Hash)(const T &),
     U (HashNode)(const shared_ptr<U> &, const shared_ptr<U> &)
>
inline std::unique_ptr<MerkleNode<T, U, Hash, HashNode>> AddLeaf(
    std::unique_ptr<MerkleNode<T, U, Hash, HashNode>> root, const T &value) {
  auto right = std::make_unique<MerkleNode<T, U, Hash, HashNode>>(value);
  return std::make_unique<MerkleNode<T, U, Hash, HashNode>>(root.release(), right.release());
}

Listing 4 — merle::MerkleNode::AddLeaf()

As you can see, most of the code there is a (rather tedious, but, alas, necessary) specification of the template types; we then proceed to create two MerkleNodes: one (right) to hold the new leaf’s node’s data, and another (which is a returned temporary, which will be moved by the compiler into the receiver’s variable) which holds in its left branch the original root, and in the right branch the newly created leaf.

Rather obviously, this results in a highly unbalanced tree:

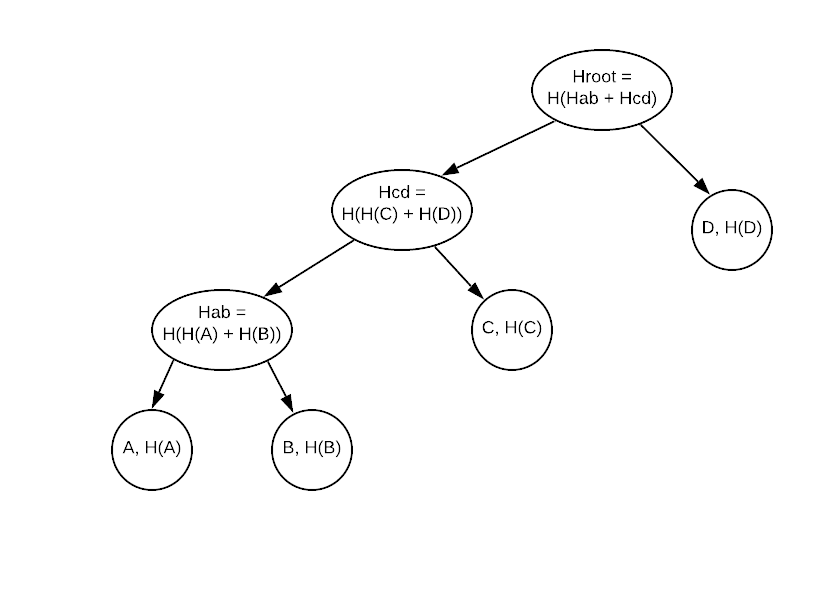
however, as the purpose of a MerkleTree is to hold data and ensure its validity against tampering or computation errors (and not, for example, search efficiency) this is a very convenient trade-off: re-balancing the tree after each (or even several) addition would require recomputing almost all of the nodes’ hashes (apart from the leaf nodes, which remain unchanged); given that this would likely require many cryptographic operations (which are notoriously CPU intensive) it would be a rather poor trade-off.

Conclusions

Merkle Trees are important data structures that allow both storage and transfer of sensitive data, ensuring validity against tampering, errors and data corruption; they can be very efficient, both computationally and for data storage and transfer.

The implementation shown here takes full advantage of features in Modern C++ (C++11 and later) to ensure no memory leaks, pointer errors and keep the code easy to maintan and simple to use for clients.

The full code listing is available here.